新着記事
数学モデルを用いたグルーピング
集団をいくつかのグループに分けて指導する時、どのように組織化するのが最適なのか、科学者は数学モデルを使用しました。
For a fresh approach to this age-old question in grouping theory, a researcher from the University of Rochester, along with his childhood friend, an education professor at the University of Nevada, Las Vegas, turned to math.
参照元:https://www.rochester.edu/newscenter/global-grouping-theory-math-strategies-students-529492/
– ロチェスター大学 University of Rochester. September 6, 2022 –
サッカーをしたい30人の子供たちがいるとします。
あなたは、彼らを2つのチームに分け、技術を練習し、コーチから学んでより良い選手になるようにしたいと思います。
しかし、子どもたちが上達するために最も効果的な方法は何でしょうか。
子どもたちを技術レベルごとにグループ分けし、最も技術の高い選手を1つのグループに、それ以外の選手をもう1つのグループにするのがよいのでしょうか。
それとも、才能と技術で2つのチームに分けるべきでしょうか?
ロチェスター大学の研究者は、ネバダ大学ラスベガス校の教育学教授という幼なじみとともに、この古くからのグループ分けの問題に対する新鮮なアプローチを求めて、数学に目を向けました。
ロチェスター大学医療センターの神経学教授で、ロチェスターの健康+技術センター(CHeT)所長のチャド・ヒートウォール氏は話します。
ヒートウォール氏:訓練目的の人選やグループ分けは、私たちの社会では極めて一般的です。指導の目的で生徒をグループ分けする最適な方法については、歴史的かつ継続的に厳密な議論が行われています。
Education Practice and Theory誌に掲載された論文で、研究チーム(ネバダ大学ラスベガス校の教授・学習学の准教授ピーター・ウィーンズ氏とCHeTのディレクター、クリスティン・ジッツィ氏も含む)は、初めて、グループ分けに対する数学的アプローチを開発したのです。
このアプローチは、さまざまなグループ分けの方法を比較し、教師主導の指導に最適なグループ分けの方法を選択するものです。
この研究は、教育だけでなく、経済、音楽、医学、スポーツの分野にも広く応用されています。
ヒートウォール氏:私たちの解決策は、純粋に数学的なレンズを通して、サンプル全体の最大の利益を評価することでした。我々の知る限り、この新しい数学的アプローチは、このように説明され、利用されたことがありません。
グループ化理論における2つのアプローチ
グローバル・グルーピング理論(グループへの個人の選択がグループのメンバーの学習やパフォーマンスにどのように影響するかを研究する学問)によると、個人をグループ化する一般的な方法は2つある。
同じような適性を持つ個人をグループ化し、一方のグループは他方のグループよりかなり高いスキルを持つようにします。
例えば、教室の読書会では、上級者はあるグループに、下級者は別のグループに振り分けられます。
クロスセクショナル・グルーピング:様々な適性を持つ個人で構成される平等なグループを形成し、すべてのグループのスキルがほぼ等しくなるようにする方法。例えば、2つのサッカーチームがあり、それぞれサッカーをしたことのある人としたことのない人で等しく構成されているとします。
この2つの一般的なグループ分けの方法を評価するために、研究者は数学的な原理と方程式を用いました。分析にあたっては、まず、複数のグループが形成されること、参加する個人のスキルレベルが異なること、最適な教育環境とは、生徒が自分のスキルレベルに合ったレベルで教えられること、最適なグループ分けシステムは、すべての生徒の集合的利益を最大化することなど、いくつかの前提条件を設定した上で行いました。
この新しいアプローチを用いて、彼らは、すべての人の学習を改善することを最終目的とする場合、同じようなスキルを持つ階層的なグループ分けは、横断的またはランダムなグループ分けよりも優れていることを発見しました。
ヒートウォール氏:数学的に言えば、同じようなスキルを持つ個人をグループ化することで、すべての個人の学習の総和が最大になることを示しました。同じようなスキルを持つ学生を一緒にすれば、講師は学生にとって高度すぎず、つまらなくないレベルで教えることができ、グループに関係なく、すべての学生の総合的な学習を最適化することができるのです。
経済学がこのアプローチの核心であり、教師対生徒の比率が高い小グループが、最適な学習にとって最も有益であることも確認されています。
ヒートウォール氏:これは数学が示していることです。
もちろん、このルールには注意点があります。
研究者のアプローチは、最終目標が全員にとって最も集合的な利益を得ることであると仮定しています。
もし最終目標が違っていたら、例えば、他のすべての運動訓練生を犠牲にして、一人のオリンピック選手を生み出すことが目標だったら、結論も最適なアプローチも違ってくるかもしれません。
ヒートウォール氏:後者の場合、一人の選手の利益や成長のために、他の選手の指導や育成をデザインすることになります。一人が最高の利益を得る一方で、他の誰も利益を得ないということになるかもしれない。しかし、私たちのアプローチはそのように設計されていません。
むしろ、「いかにして全員を育てるか」という視点でアプローチしているという。「どうすれば、生徒全員が最も恩恵を受けられるような教育状況を作り出せるか」。
ヒートウォール氏は、研究者の結論が議論を呼ぶかもしれないことを認識していますが、このアプローチは、数学が日常の問題を解決するための偏りのない方法を提供できることを説明していると述べています。
ヒートウォール氏:それが、この研究の素晴らしいところです。私たちは、ただ事実を並べて、これが仮定で、これが数学的アプローチで、これが数学が示すものだと言っているのです。これは、数学と科学が古くからの疑問を解決し、すべての関係者の学習、成長、可能性を促進するのに役立つという実例なのです。


この記事が気に入ったら
いいね または フォローしてね!
関連記事
新着記事
-

 男女ともに長生きになる「男女平等」2023.03.07健康
男女ともに長生きになる「男女平等」2023.03.07健康 -

 他者を犠牲にして利益を取る・利益を度外視して他者への害を取り除く2023.03.06人体・脳
他者を犠牲にして利益を取る・利益を度外視して他者への害を取り除く2023.03.06人体・脳 -

 「寿命を延ばす」良質な睡眠2023.03.05健康
「寿命を延ばす」良質な睡眠2023.03.05健康 -

 見極める力を養う「チャットボットの精度」2023.03.04技術
見極める力を養う「チャットボットの精度」2023.03.04技術 -

 健康増進と生きがいにつながる「森林浴」2023.03.03健康
健康増進と生きがいにつながる「森林浴」2023.03.03健康 -

 米国の6人に1人「肥満による死」2023.03.02健康
米国の6人に1人「肥満による死」2023.03.02健康 -

 週休4日制で生産を維持する2023.03.01社会
週休4日制で生産を維持する2023.03.01社会 -

 オンライン学習で学生に届く教育方法2023.02.28学習
オンライン学習で学生に届く教育方法2023.02.28学習 -

 学業成績に影響を与える「夜間の睡眠」2023.02.27健康
学業成績に影響を与える「夜間の睡眠」2023.02.27健康 -

 心の豊かさに大きく影響を与える「目的意識を持った10代の若者」2023.02.26健康
心の豊かさに大きく影響を与える「目的意識を持った10代の若者」2023.02.26健康
よく読まれている記事
-

 なぜタイピングより手書きの方が、記憶に定着するのか
なぜタイピングより手書きの方が、記憶に定着するのか -

 どんな曲が好き?「 音楽の好みと性格の関連性は普遍的 」
どんな曲が好き?「 音楽の好みと性格の関連性は普遍的 」 -

 視覚と意思決定領域の結びつきが強い「鮮明なイメージ能力がある人」
視覚と意思決定領域の結びつきが強い「鮮明なイメージ能力がある人」 -

 「触覚が敏感な部位はなぜあるのか」触覚メカニズムが解明される
「触覚が敏感な部位はなぜあるのか」触覚メカニズムが解明される -

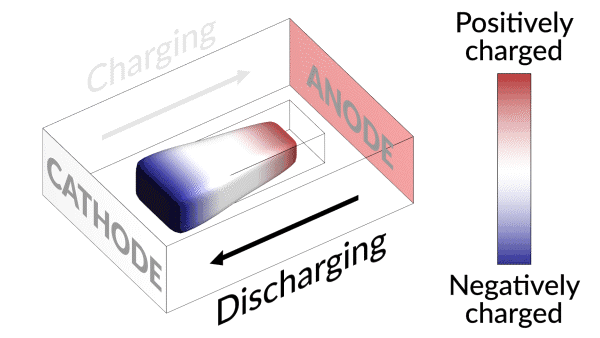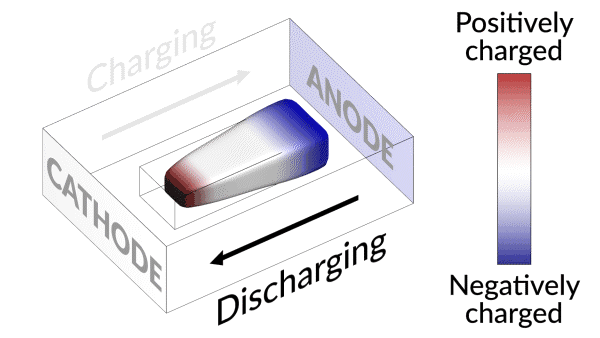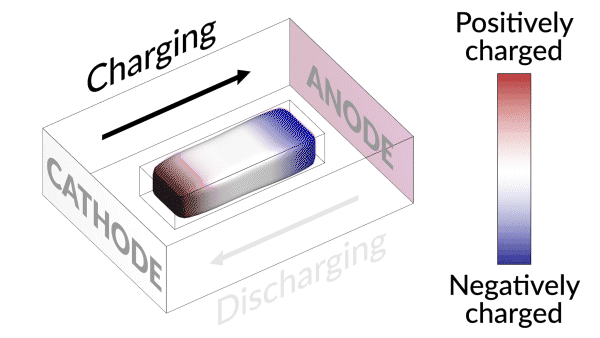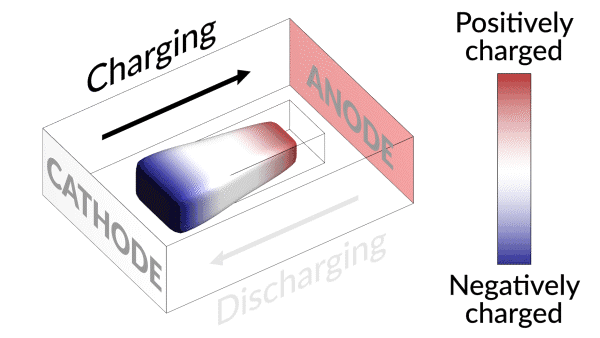 不活性化されたリチウムイオン電池を甦えさせる「復活するリチウムイオン電池」
不活性化されたリチウムイオン電池を甦えさせる「復活するリチウムイオン電池」 -

 記憶が脳に保存される新しい理論「MeshCODE理論」が開発される
記憶が脳に保存される新しい理論「MeshCODE理論」が開発される -

 大面積有機フォトダイオードに置き換わる?「シリコンフォトダイオード技術」
大面積有機フォトダイオードに置き換わる?「シリコンフォトダイオード技術」 -

 幸福度を7%上げる「旅行の仕方」
幸福度を7%上げる「旅行の仕方」 -

 「世界最長寿記録を更新し132歳まで生きる人が出現する」ベイズ統計学予測
「世界最長寿記録を更新し132歳まで生きる人が出現する」ベイズ統計学予測 -

 組織の中で行われたインシビリティ(非礼な言動)を軽視してはいけない理由
組織の中で行われたインシビリティ(非礼な言動)を軽視してはいけない理由
N E W S & P O P U L A R最 新 記 事 & 人 気 記 事
WHAT'S NEW !!
-






男女ともに長生きになる「男女平等」
【男女ともに長生きになる「男女平等」】 権利とは人間が作り出した構造ですが、男女平等が進むと男女ともに長生きになるようです。 The first global study to investi... -






他者を犠牲にして利益を取る・利益を度外視して他者への害を取り除く
【他者を犠牲にして利益を取る・利益を度外視して他者への害を取り除く】 他者を犠牲にして自分の利益を選ぶ、自分にとって利益は少ないが他者への害を防ぐ、道徳的なに... -






「寿命を延ばす」良質な睡眠
【「寿命を延ばす」良質な睡眠】 良質な睡眠をとることは、寿命を何年も長くする可能性があります。 Getting good sleep can play a role in supporting your heart and... -






見極める力を養う「チャットボットの精度」
【見極める力を養う「チャットボットの精度」】 ChatGPTをはじめ、チャットボットの精度は人が書いたものかどうかわからない程までの水準になっています。 The most rec...
-






なぜタイピングより手書きの方が、記憶に定着するのか
【なぜタイピングより手書きの方が、記憶に定着するのか】 ノルウェー科学技術大学の研究によると、手書きの方が物事をよく覚えることが判明しました。 様々なコンピュ... -






どんな曲が好き?「 音楽の好みと性格の関連性は普遍的 」
【どんな曲が好き?「 音楽の好みと性格の関連性は普遍的 」】 激しい音楽を好んで聴く人は、激しい性格の持ち主なのでしょうか?研究者は、音楽の好みと性格の関連性は... -






視覚と意思決定領域の結びつきが強い「鮮明なイメージ能力がある人」
【視覚と意思決定領域の結びつきが強い「鮮明なイメージ能力がある人」】 鮮明にイメージできる人は、視覚ネットワークと意思決定に関連する脳の領域が強く結びついてい...
News
- 新着記事 -
Popular
- 人気記事 -
H A P P I N E S S幸 福
人気 (❁´ω`❁)
M E A L食 事
B R A I N脳
人気 (❁´ω`❁)
H E A L T H健 康
人気 (❁´ω`❁)
-






人体・脳
健康な脳を保ち老化を遅らせる「アマゾンの先住民族ツィマネ族の生活習慣」
【健康な脳を保ち老化を遅らせる「アマゾンの先住民族ツィマネ族の生活習慣」】 ボリビア・アマゾンの先住民族であるツィマネ族が、アメリカやヨーロッパの人々に比べて... -






社会
自制心が健康と若さをもたらす理由
【自制心が健康と若さをもたらす理由】 デューク大学の研究チームは、自制心が心身に及ぼす影響を調査しました。 1000人を出生から45年間に渡って追跡した大規模調査で... -






健康
高強度インターバルトレーニングは、適度な運動よりも心臓を強化する
【心臓を強化する高強度インターバルトレーニング】 ノルウェー科学技術大学の研究によると、トレーニングの強度が、病気の重症度を軽減し、心臓機能を改善し、作業能力...
-






人体・脳
健康な脳を保ち老化を遅らせる「アマゾンの先住民族ツィマネ族の生活習慣」
【健康な脳を保ち老化を遅らせる「アマゾンの先住民族ツィマネ族の生活習慣」】 ボリビア・アマゾンの先住民族であるツィマネ族が、アメリカやヨーロッパの人々に比べて... -






社会
自制心が健康と若さをもたらす理由
【自制心が健康と若さをもたらす理由】 デューク大学の研究チームは、自制心が心身に及ぼす影響を調査しました。 1000人を出生から45年間に渡って追跡した大規模調査で... -






健康
高強度インターバルトレーニングは、適度な運動よりも心臓を強化する
【心臓を強化する高強度インターバルトレーニング】 ノルウェー科学技術大学の研究によると、トレーニングの強度が、病気の重症度を軽減し、心臓機能を改善し、作業能力...
J O B仕 事
人気 (❁´ω`❁)
-






社会
週休4日制で生産を維持する
-






人体・脳
アイデアや閃きが降りてくる「横断的なコミュニケーション」
-





社会
大災害を読み解く鋭い解決策
-






思考・瞑想
賞や表彰が発明家の創造性を低下させる
-






人体・脳
創造的な人はここが違う!「非創造的なハブを回避し非典型的なアプローチをする」
-






社会
アメリカ陸軍で既に多数の成功を収めている「人々を創造的にするトレーニング」
-






社会
2年は普及しない?「カテゴリーイノベーション戦略」
-






社会
管理者級以上必見「創造性を引き出す同僚間の友情とサポートを育む組織づくり」
-






社会
アイデアを創出する人数「少人数のグループのほうが新しいアイデアが出やすい」
-






健康
散った気を元の集中に戻す「1日最大50%費やす迷いを断つマインドフルネス」
-





社会
移動によるエネルギーが激減「環境に優しく誰でも参加できるオンライン会議」
-






社会
山火事コスト数十億ドルのコスト削減「インドネシアの泥炭地回復」
-






社会
価格末「99円」設定が販売者に不利益を及ぼす驚愕の理由
-






社会
購買意欲を掻き立てる商品提示方法
-






社会
「感情的異質性」がチームの創造性を高める
-






社会
従業員の創造性を高める驚愕の方法「報酬を選択制にする」
-






社会
テクノロジーの力でセレンディピティを生み出す
-






社会
様々なテーマの問題への取り組みにつながる「ダ・ヴィンチ構想」
-






社会
改善が必要な状況に「やめる」という解決策がでない理由
-






社会
空想が苦手な理由と、その修正方法
-






学習
パズル解きの極意、最良の選択より優れた驚愕の方法
-






社会
大麻が独創的で実現不可能なアイデアを創出するという実験結果
-






社会
記憶に残るユーモアを含んだニュース
-





社会
なぜメッセージと画像が一致してない情報は伝わらないのか
-






社会
消費者を購買に結びつける音楽
-






技術
自動化工場などの緊急事態に備えて知識を生かしておく方法
-






社会
「生産性も顧客満足度も向上」プロジェクトに自主性を持たせる
-






人体・脳
人は1日に35,000回の意思決定をしている「意思決定を行うアルゴリズム」
-






社会
他文化と頻繁衝突する文化圏は協力的なゲームが流行?「ゲームからみる文化」
-






社会
「通勤はわるいもの?」モバイルセンシングで仕事の成果と通勤の関連性を解明
-






社会
テクノロジーは労働者の幸福度にどのような影響を及ぼすか
-






社会
雇用の創出ではなく雇用の置換が進む「ロボットなどの作業の自動化」
-






社会
「柔軟で弾力性のある対応が可能」生物系を模倣した多様なサプライチェーン
-






社会
「患者のメンタルヘルスケアを向上させる」患者と心理療法士のマッチング
-




学習
デジタルデバイス用に最適なフォント「AdaptiFont」
T E C H N O L O G Y技 術
人気 (❁´ω`❁)